33
20
La Lettre
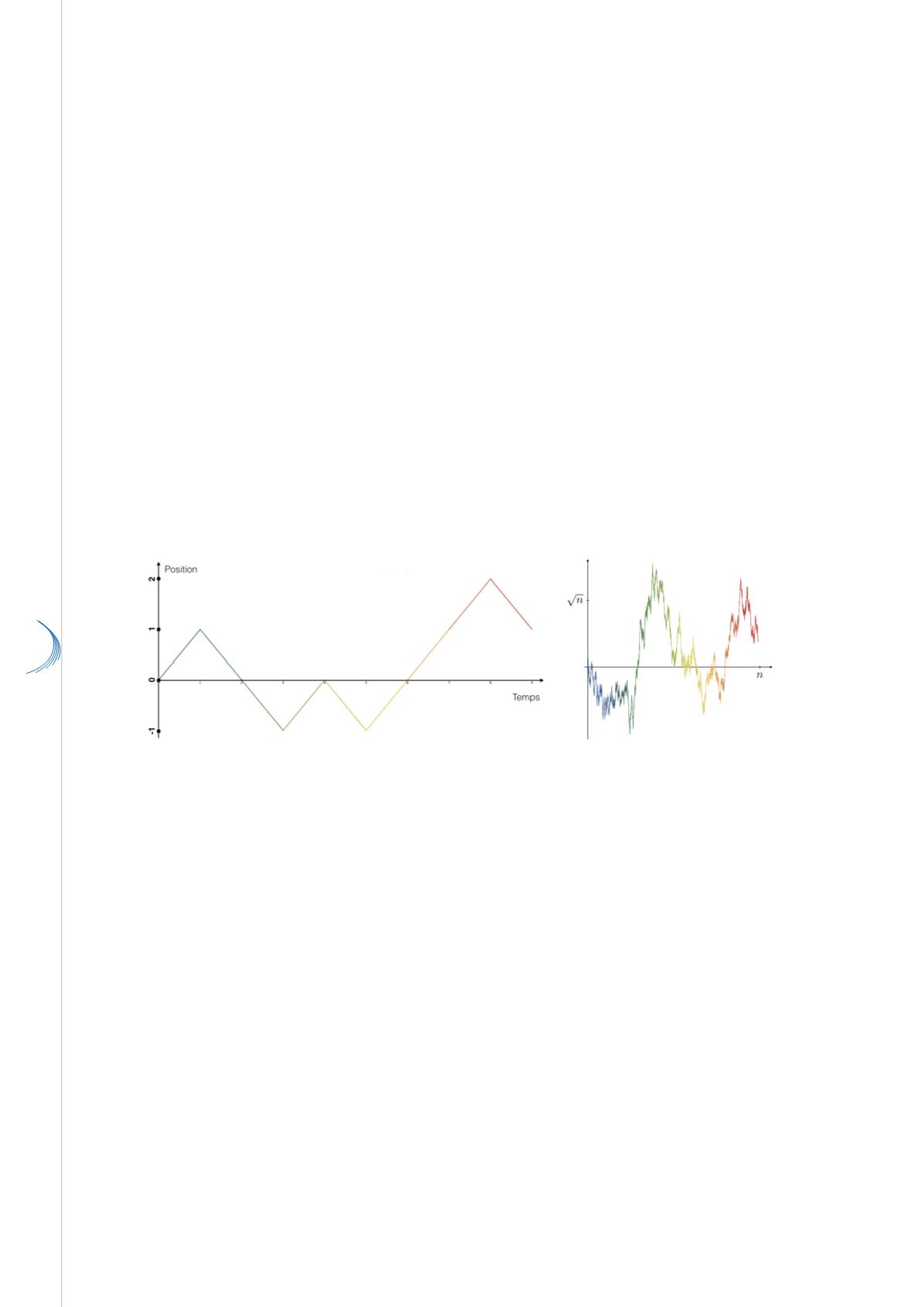
Une marche aléatoire de 9 pas (à gauche) et une marche aléatoire de 20 000 pas (à droite). La couleur de
la particule évolue du bleu au rouge au cours du temps. Dans la figure de droite, une courbe aléatoire très
irrégulière apparaît : c’est le mouvement brownien en dimension 1.
© DR
Et les maths dans tout cela ?
Dans les années 1920, le brownien, comme l’appellent de nos jours les probabilistes, est un pilier de la
physique, mais n’a pas encore de définition mathématiquement précise. Il faudra attendre les travaux de
Norbert Wiener pour donner un sens à cette fonction continue aléatoire. Un temps baptisé « processus
de Wiener », le « mouvement brownien » doit finalement sa terminologie à Paul Lévy, fondateur des
probabilités françaises ; il est, depuis, l’un des outils les plus puissants des probabilistes. Si la définition
mathématique précise du brownien est assez délicate, on peut en avoir une bonne intuition en décrivant
son analogue discret : la marche aléatoire. Le mouvement continu est transformé en une suite de pas
indépendants. Dans le cas le plus simple, on considère sur une ligne discrète {…, -2, -1, 0, 1, 2, 3, ...} une
particule qui, démarrant initialement de 0, saute à pile ou face vers la droite (+1) ou vers la gauche (-1)
avec une probabilité égale. Sa position à l’instant
n
est notée
X
n
. Si l’on représente graphiquement
X
n
en
fonction de
n
, quand
n
tend vers l’infini, une fonction aléatoire apparaît : c’est le mouvement brownien en
dimension 1.
Il faut noter que les échelles choisies pour le déplacement de la particule et pour le temps ne sont pas les
mêmes : ainsi, après
n
pas (
n
grand), la particule se trouve à une position aléatoire typiquement d’ordre
√n
. Cette loi d’échelle du mouvement brownien est fondamentale et apparaît dans les calculs d’Einstein et
Smoluchowski. C’est cette même loi d’échelle qui se manifeste dans le théorème central limite, qui peut
s’énoncer ainsi : la loi de position aléatoire
X
n
divisée par
√n
converge vers la loi de Gauss, dont la densité
de probabilité est la fameuse courbe en cloche. Le mouvement brownien peut donc être vu comme une
version dynamique ou trajectorielle du théorème central limite. Après avoir donné sa définition formelle,
Wiener et ses acolytes étudièrent les propriétés fines du mouvement brownien. Ils montrèrent que bien
qu’aléatoire, cette fonction obéit à des lois déterministes, c’est-à-dire indépendantes du hasard. Ainsi,
pour toutes les réalisations possibles du mouvement brownien en dimension 1, cette fonction, bien que
continue, n’admet pas de tangente et oscille frénétiquement « de la même manière » : c’est une courbe
fractale de dimension 3/2.


